시계열 분석 : 정상성(Stationary) / AR, MA / ACF, PACF

1. 일변량 시계열 모형 (Univariate Time Series Model)

• 이론에 기반하지 않음 (a-theoretical model)
• 구조 모형이 제 기능을 하지 못할 때 사용
  • 어떤 변수의 변화 설명 시 이 변수를 움직여 나가는 변수들을 관찰할 수 없거나 측정이 불가능 한 경우 또는 해당 변수보다 더 낮은 빈도로만 측정 가능한 경우 (ex. GDP)

2. 시계열 관련 용어 간단 정리

1.  정상성 (Stationary)
   • 시간이 지나도 평균, 분산이 일정한 데이터의 성질
   • 계절성, 추세성과 상반되는 개념
   • 정상성을 만족하는 데이터가 분석에 용이하므로 비정상성인 데이터는 차분(differencing)을 통해 정상성 시계열 데이터로 변환
2.  White Noise Process
   • 고정된 평균와 분산을 가짐 => 정상성을 가짐

 

  < 정상성 확인 방법 >

1. ACF (autocorrelation function)
   • t+k 기간 이전의 변수와 현재 시점(t) 변수간의 자기상관
   • 시차가 커질수록 ACF는 0에 가까워짐 (데이터 간 상관관계 down)
     • 정상 시계열 : ACF 값이 빠르게 0에 가까워짐

1. PACF (partial autocorrelation function)
   • 현재(t) 변수와 과거의 특정 시점(t-k)간의 상관관계 측정 시, 이 두 기간 사이의 모든 변수(t-1, t-2, .. t-k+1)의 영향을 제거한 다음 상관관계 측정한 자기상관

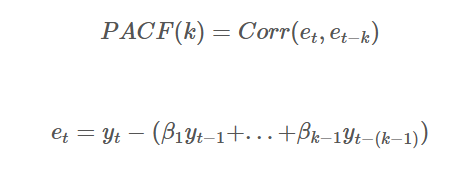
3. 기본적 시계열 모형

 - MA(q), Moving Average

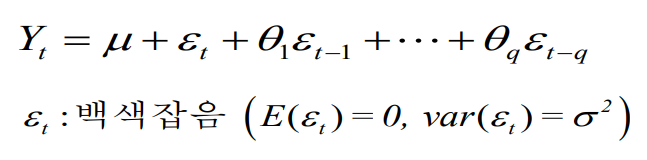
• 오늘 시장에 들어온 충격(e, 백색 잡음)의 가중 평균
• 계수와 무관하게 정상성을 가짐
• ACF를 가지고 알 수 있음

     ex) 오늘의 삼성전가 주가 예측을 위해 그 전까지의 삼성전자의 주가 예측 오차를 활용

 

 

 - AR(p), Autoregressive process

• 오늘의 주가를 모델링하기 위해 이전의 관측값을 사용하는 모델
• PACF를 고려해야함
• p : PACF가 0으로 되기 직전 값

      ex) 오늘의 삼성전가 주가 예측을 위해 그 전까지의 삼성전자의 주가 데이터를 활용

 

 

---

본 자료는 중앙대학교 블랙스톤 금융AI 아카데미 (Blackstone Financial AI Academy) 코딩 부트 캠프 강의 자료를 참고하여 제작하였습니다.